Un equipo de investigadores británicos y suizos han creado los que, probablemente, sean los laberintos más difíciles de resolver. Describen las estructuras de los cuasicristales

R. Badillo / El Confidencial
Girolamo Frigimelica diseñó y construyó en el año 1720 el que presume de ser el laberinto más difícil del mundo. Se encuentra en Villa Pisani, Italia, y cuenta con nueve aros concéntricos formados por setos tan altos que es imposible ver algo por encima de ellos. La leyenda dice que hasta el mismísimo Napoleón fue superado por el reto de resolverlo. Llegar a su centro tiene como premio subir a una torre desde la cual ver el laberinto en todo su esplendor.
Aunque realmente no fuese así, un equipo de físicos británicos y suizos parece que se plantearon el desafío de superar la creación de Girolamo Frigimelica. Para ello, emplearon principios de geometría fractal y lo combinaron con los movimientos en forma de ‘L’ de los caballos en el ajedrez. Después, lo combinaron con rutas hamiltonianas y mosaicos de Ammann-Beenker para crear los laberintos más complejos que se han elaborado hasta la fecha.
Eso sí, la creación de estos laberintos no era el objetivo inicial de este estudio, que ha sido dirigido por Felix Flicker y en el que han participado los físicos Shobhna Singh, de la Universidad de Cardiff, y Jerome Lloyd, de la Universidad de Ginebra. Se encuentra publicado en la revista Physical Review X y, a través de él, pretendían describir la «exótica» forma de los cuasicristales, un tipo de materia que se encuentra muy raramente en la naturaleza y que son híbridos de cristales ordenados y desordenados.
Cómo los han creado
El citado Felix Flicker, que trabaja como físico en la Universidad de Bristol, afirmó que “cuando observamos las formas de las estructuras que construimos, no tardamos en darnos cuenta de que se generaban laberintos extraordinariamente intrincados. Sus tamaños crecen de forma exponencial y hay un número infinito de ellos».
La sal, el cuarzo o el diamante son ejemplos de cristales ordenados, ya que sus átomos dibujan patrones muy claros. En cambio, el vidrio y ciertas formas de hielo forman cristales desordenados. Los átomos de los cuasicristales parecen formar un patrón, pero al estudiarlo detalladamente es posible darse cuenta de que no se repite con exactitud.
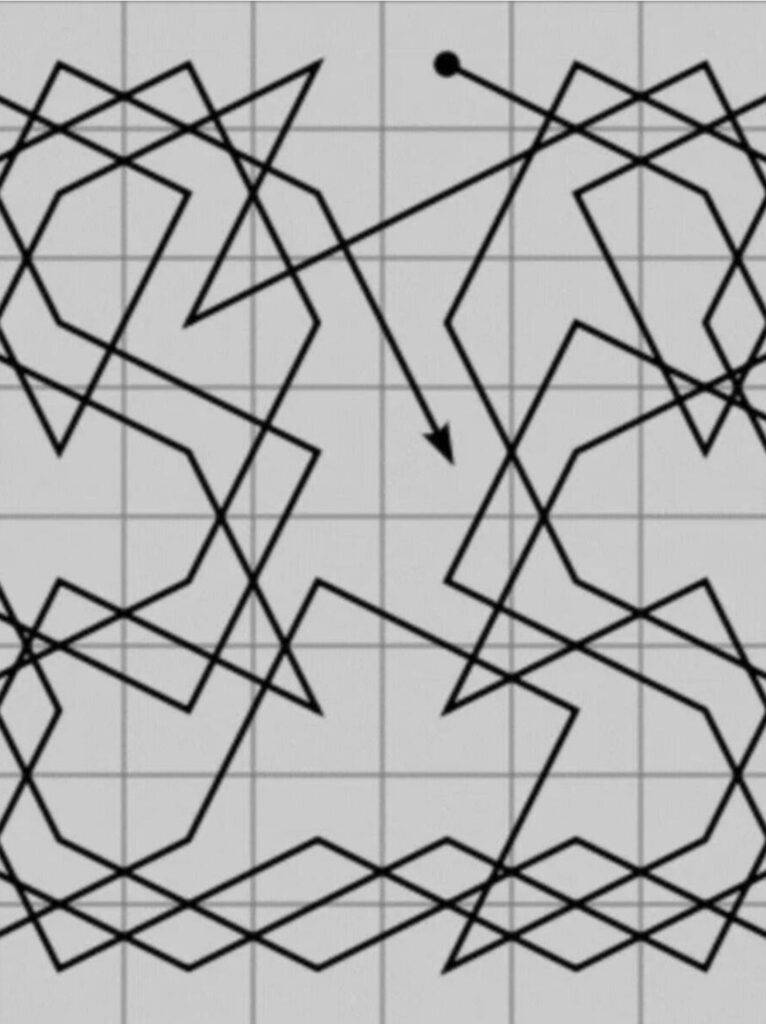
El proyecto se inspira en el movimiento del caballo en el ajedrez, una pieza que se desplaza en forma de ‘L’ (dos casillas en una dirección y una en ángulo recto), visitando cada casilla del tablero solo una vez antes de regresar a su posición inicial. Este recorrido se denomina ciclo hamiltoniano y es clave para el diseño del laberinto.

Utilizando mosaicos de Ammann-Beenker, Flicker y sus colegas lograron generar ciclos hamiltonianos que conectan cada átomo del cuasicristal en una sola línea continua que nunca se cruza. Este diseño se puede escalar indefinidamente, creando patrones fractales donde las partes más pequeñas reflejan la estructura de las más grandes.
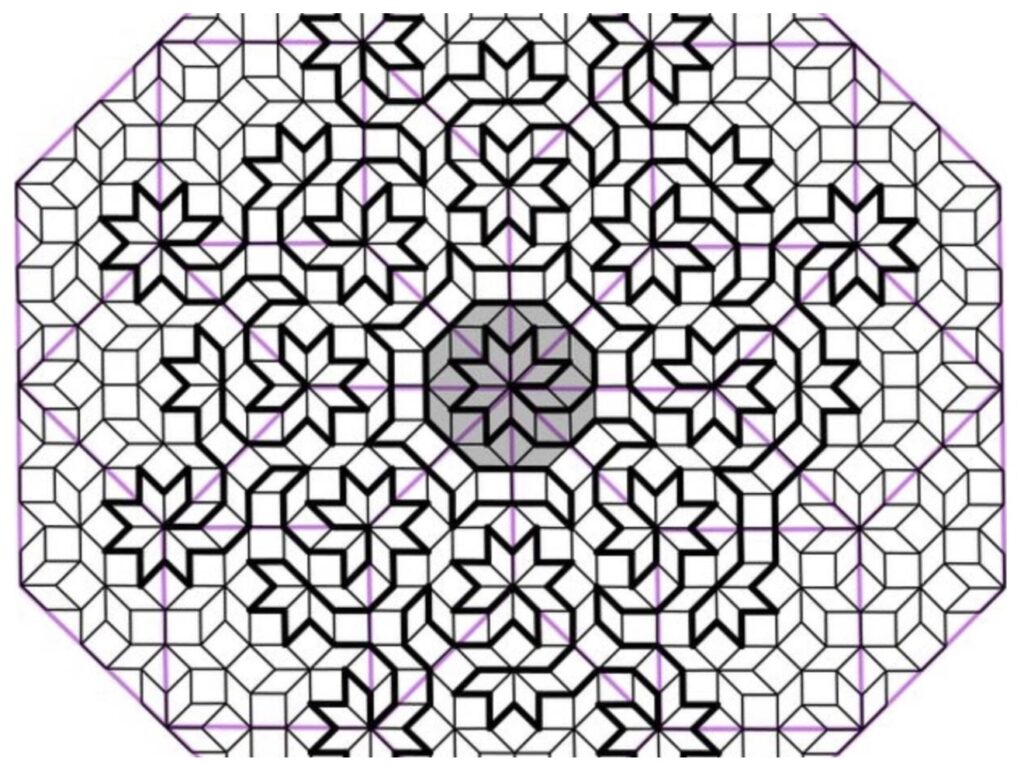
La creación de estos laberintos no solo representa un desafío intelectual, sino que también tiene importantes implicaciones prácticas. La capacidad de encontrar ciclos hamiltonianos puede ayudar a resolver problemas matemáticos complejos, como la optimización de rutas y el plegamiento de proteínas. Además, los cuasicristales podrían mejorar los procesos de captura de carbono mediante adsorción, ya que su estructura única permite un mayor empaquetamiento de moléculas flexibles.

