El anterior año cuadrado fue 1936, y el próximo no llegará hasta 2116. Pero, ¿qué significa esto? Te lo contamos.

FERNANDO BLASCO / National Geographic
El año que comienza es un año cuadrado: 2025 = 45². No decimos que eso sea bueno ni malo, porque el anterior año cuadrado fue 44² = 1936, que no brilla precisamente por ser un año de paz. Pero lo que sí podemos afirmar es que, para la mayoría de nosotros, 2025 será el único año cuadrado en el que vivamos: algunos mayores sí que vivían en 1936 y algunos de los más jóvenes de hoy puede que lleguen al 2116.

Noticia relacionada
Ni asteroide, ni cometa: Webb capta un objeto nunca antes visto
Sarah Romero
Comencemos con un pequeño juego. En el calendario de enero de 2025 marque un cuadrado de tamaño 4×4. Tiene 4 posibilidades:
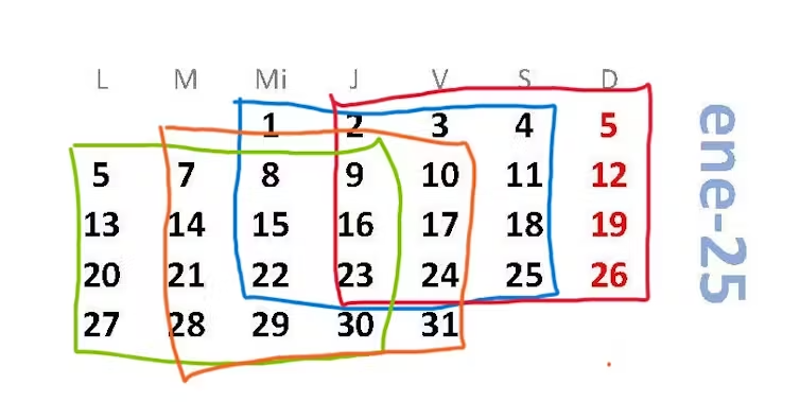
Sume los números que aparecen en los vértices del cuadrado que ha elegido y apunte ese número.
Elija ahora uno de los números del interior del cuadrado, rodéelo con un círculo y tache todos los que están a izquierda y derecha y arriba y abajo del que ha señalado.
De entre los números que están sin tachar (ni rodear), elija un segundo número. Márquelo también con un círculo y tache los que están por encima de él, por debajo, a su izquierda y a su derecha.
De los que quedan sin tachar ni rodear elija uno, rodéelo y, de nuevo, tache los que están en su misma fila y columna.
Ya le quedan pocos números sin usar. Elija uno de ellos, enciérrelo con un círculo, y tache todos los que queden sin usar en el cuadrado.
Sume los números que había metido en los círculos.
¿Coincide esa cantidad con la que había escrito antes? ¿Sorprendente?
Por qué coincide la cifra
El hecho de rodear números y tachar los que se encuentran en la misma fila o columna fuerza a que se elijan 4 números con una propiedad importante: cada uno de los números encerrados con un círculo está en una fila diferente y, a la vez, en una columna diferente.
Así, entre los 4 números se barren todas las filas y todas las columnas. Por otra parte, los números de la segunda fila se obtienen sumando 7 a los de la primera fila. Los de la tercera se obtienen añadiendo 14 y los de la cuarta sumando 21 a los de la primera. Si llamamos “a” al vértice superior izquierdo, los demás números de esa fila serán a+1, a+2 y a+3. Si, por ejemplo, los números elegidos fueran los de la diagonal, la suma sería a+(a+1+7)+(a+2+14)+(a+3+21). Cualquier elección que hagamos nos llevará a esa misma suma (aunque expresada en un orden diferente). No es magia. Son matemáticas.
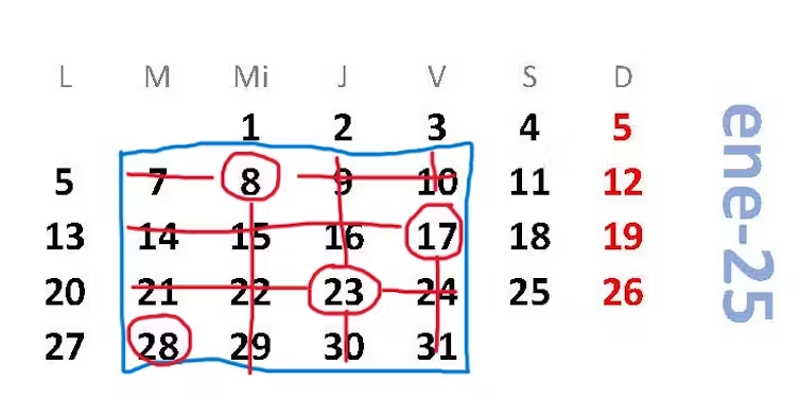
Por ejemplo, esta imagen representa a = 7 y la suma descrita sería (a+1)+(a+3+7)+(a+2+14)+(a+21)
1 de enero de 2025
Hay un desfase entre el 1 de enero y el primer día de cada uno de los otros meses. Dicho desfase se produce porque, salvo febrero en años no bisiestos, los meses no constan de semanas completas.
Maurice Kraitchik menciona en su libro Mathematical Recreations una fórmula ideada por Carlos Federico Gauss para poder determinar el día de la semana, pero es mucho más versátil y rápida la que descubrió Lewis Carroll y que fue publicada en Nature como nota corta. El método de Carroll requiere hacer algunos cálculos: básicamente dividir entre 4 y entre 7 y quedarnos con los restos.
En 2020 Miquel Durán, profesor de química y entusiasta divulgador, y yo mismo adaptamos los cálculos de Carroll a un esquema gráfico en el que para determinar el día de la semana en que cae una fecha no hay más que contar con los dedos. Este es nuestro calendario perpetuo:
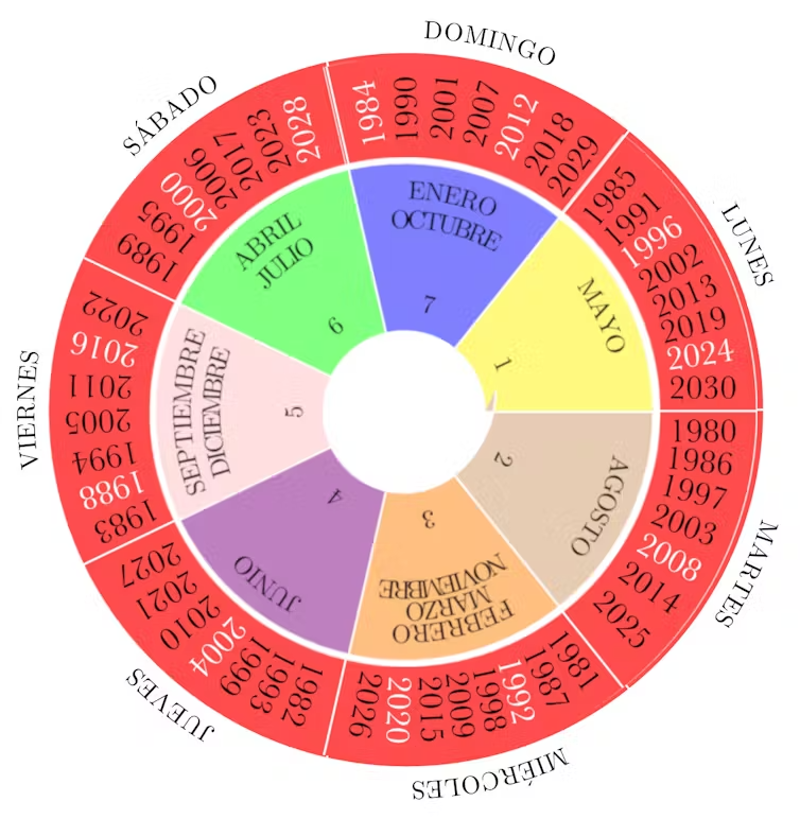
Calendario perpetuo.
- Elija el año. Atención, los años bisiestos están escritos con tinta blanca. Ponga su dedo índice sobre el año elegido.
- Busque el mes. Verá un número debajo del mes. Muévase en el sentido de las agujas del reloj tantos pasos como indica el número que está bajo el mes.
- Muévase en el sentido de las agujas del reloj tantas veces como indique el número del día de la fecha que ha elegido.
- Precaución: si el año elegido era bisiesto y el mes es enero o febrero, debe moverse una posición hacia atrás.
El lugar donde está ahora su dedo índice indica el día de la semana en que cae la fecha elegida.
El orden de los días
El día 1 de enero de 2025 es miércoles, el día de Mercurio.
El origen del nombre de los días de la semana es bastante conocido: Luna, Marte, Mercurio, Júpiter, Venus. Sábado y domingo nos descuadran la idea astronómica por tratarse de nombres religiosos: el Sabbat y el Dies Domini. En latín sí estaban las referencias a Saturno y Sol, que se mantienen en inglés todavía hoy.
Rob Eastaway comenta en su libro How Long is a Piece of String la razón del orden en el que aparecen los días de la semana. Los datos conocidos de los que partimos son los tiempos que tardan los objetos celestes, desde nuestro punto de vista, en dar una vuelta y volver a la posición inicial: Saturno tarda 28 años; Júpiter, 12 años; Marte, 687 días; el Sol, 365 días; Venus, 225 días; Mercurio, 88 días, y la Luna, 28 días. Podríamos haber puesto los nombres de los días de la semana por este orden y haber acabado, pero ese no es el orden que utilizamos.
La clave del orden en el que aparecen mencionados los días de la semana se debe a que los babilonios nombraron las horas, no los días, según los periodos de las órbitas, de mayor a menor. Así, escribieron las 24 horas del día asignando esos nombres:
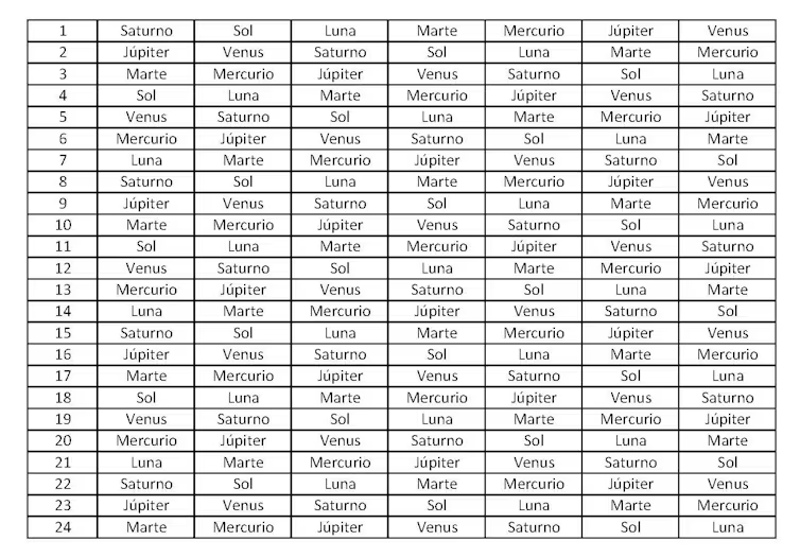
En vertical las horas, en horizontal los siete días de la semana. La primera hora del primer día de la semana fue asignada a Saturno y las siguientes a Júpiter, Marte, el Sol, Venus, Mercurio y la Luna respectivamente. La primera hora del segundo día de la semana se asignó al Sol, manteniendo la misma rotación el resto de las horas y días.
Si nos fijamos en una línea cualquiera de esa tabla veremos el orden habitual en el que aparecen los días de la semana.
El final de un año y el principio de otro nos evoca muchos sentimientos: hacemos balance de lo que ha pasado y también propósitos para el nuevo periodo que comienza. Podríamos hacerlo en cualquier momento pero, como todo ritual, bien merece una ocasión solemne.
2025 puede ser el único año cuadrado de nuestras vidas. ¡Habrá que celebrarlo!
Fernando Blasco, Profesor Titular de Universidad de Matemática Aplicada. Área de interés: educación, divulgación y comunicación científica, Universidad Politécnica de Madrid (UPM)
Este artículo fue publicado originalmente en The Conversation. Lea el original.
